Answer:
The system has no solution
Explanation:
we have
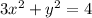 ------> equation A
------> equation A
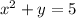 -----> equation B
-----> equation B
we know that
The solution of the system of equations is the intersection points both graphs
Using a graphing tool
see the attached figure
The figure has no point of intersection
therefore
The system has no solutions