Question

Which of the graphs below represent the function f(x) = − x3 + 4x2 − x + 3? You may sketch the graph to compare.

graph going through x axis at 3.5, Passes through y axis at 0.
graph going through x axis at negative 4.5. Passes through y axis at 0.
graph going through x axis at negative 4.5. Passes through y axis at 3.
graph going through x axis just before 4. Passes through y axis at 3.

Answer 1

Answer: Graph going through x axis just before 4 and passes through u axis at 3.

Explanation:

Given : f(x) =
`-x^(3) +4x^(2) -x +3`.

To find : graph .

Solution : We have given that f(x) =
`-x^(3) +4x^(2) -x +3`.

We can see from the given polynomial leading coefficient is negative and degree is odd.

By the end behavior of polynomial function : left end of graph would be up and right would be down .

For y intercept , plug x =0 in given function .

f(x) =
`-(0)^(3) +4(0)^(2) -(0) +3`.

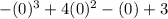f(x) = 3.

For x intercept , plug f(x) = 0.

0 =
`-x^(3) +4x^(2) -x +3`.

x = 3.92

Therefore, Graph going through x axis just before 4 and passes through u axis at 3

Answer 2

Please see the attachment.

Explanation:

`\text{Given function:}f(x)=-x^3+4x^2-x+3`

Now we find the x and y intercept of f(x)

For x-intercept: Put f(x)=0 and solve for x

So, x=3.92 (Just before 4 on x-axis)

For y-intercept: Put x=0 and solve for f(0)

So, y=3 (Passes through y-axis at 3)

End Behavior: Third degree function

`x\rightarrow -\infty , f(x)\rightarrow \infty`

`x\rightarrow \infty , f(x)\rightarrow -\infty`

Possible graph of the f(x). Please see the attachment.