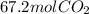Question

The acetylene tank contains 35.0 mol C2H2, and the oxygen tank contains 84.0 mol O2.

How many moles of CO2 are produced when 35.0 mol C2H2 react completely? How do you get 35.0 mol out of C2H2?

Answer 1

Answer : The number of moles of
`CO_2` produced are, 70 moles

Solution : Given,

Moles of
`C_2H_2` = 35 mole

Moles of
`O_2` = 84 mole

The balanced chemical reaction will be,

`2C_2H_2+5O_2\rightarrow 4CO_2+2H_2O`

From the balanced reaction, we conclude that

As, 2 moles of acetylene react completely to give 4 moles of carbon dioxide

So, 35 moles of acetylene react completely to give
`\farc{4}{2]* 35=70` moles of carbon dioxide

Therefore, the number of moles of
`CO_2` produced are, 70 moles

Answer 2

Answer:- As per the question is asked, 35.0 moles of acetylene gives 70 moles of carbon dioxide but if we solve the problem using the limiting reactant which is oxygen then 67.2 moles of carbon dioxide will form.

Solution:- The balanced equation for the combustion of acetylene is:

`2C_2H_2(g)+5O_2(g)\rightarrow 4CO_2(g)+2H_2O(g)`

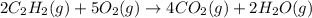
From the balanced equation, two moles of acetylene gives four moles of carbon dioxide. Using dimensional analysis we could show the calculations for the formation of carbon dioxide by the combustion of 35.0 moles of acetylene.

`35.0molC_2H_2((4molCO_2)/(2molC_2H_2))`

=
`70molCO_2`

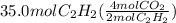
The next part is, how we choose 35.0 moles of acetylene and not 84.0 moles of oxygen.

From balanced equation, there is 2:5 mol ratio between acetylene and oxygen. Let's calculate the moles of oxygen required to react completely with 35.0 moles of acetylene.

`35.0molC_2H_2((5molO_2)/(2molC_2H_2))`

=
`87.5molO_2`

Calculations shows that 87.5 moles of oxygen are required to react completely with 35.0 moles of acetylene. Since only 84.0 moles of oxygen are available, the limiting reactant is oxygen, so 35.0 moles of acetylene will not react completely as it is excess reactant.

So, the theoretical yield should be calculated using 84.0 moles of oxygen as:

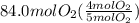
`84.0molO_2((4molO_2)/(5molO_2))`

=
`67.2molCO_2`