Question

Which of the following is a root of the polynomial shown below? f(x)=x^3-x^2-9x+9

(Points : 2)
-9

-3

2

9

Answer 1

-3 is the best answer i hope it helps

Explanation:

Answer 2

We have been given a polynomial function
`f(x)=x^3-x^2-9x+9`. We are asked to choose the root of the function from given choices.

Let us set our polynomial equal to 0.

`x^3-x^2-9x+9=0`

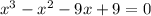
Now we will factor our polynomial by grouping method.

`(x^3-x^2)+(-9x+9)=0`

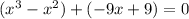
Let us factor out greatest common factor from each group.

`x^2(x-1)-9(x-1)=0`

`(x-1)(x^2-9)=0`

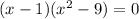
We can further factor
`(x^2-9)` using difference of squares.

`(x-1)(x^2-3^2)=0`

`(x-1)(x+3)(x-3)=0`

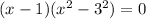
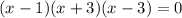
Using zero product property, we will get:

`(x-1)=0\text{ (or) }(x+3)=0\text{ (or) }(x-3)=0`

`x=1\text{ (or) }x=-3\text{ (or) }x=3`

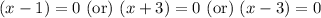
Upon looking at our given choices, we can see that
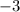`-3` is the correct choice, therefore,
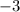`-3` is root of the given polynomial.