Answer with explanation:
For a function f(x), it is given that following Statement hold.
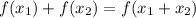
Coming to the options
(A)f(x)=x+1
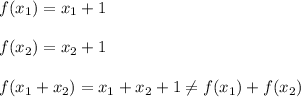
This function does not define f.
(B)f(x)=2x
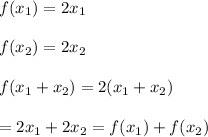
This function defines f.
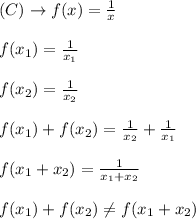
This function does not define f.
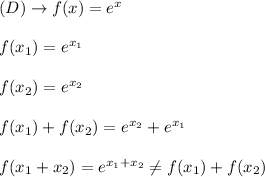
This function does not define f.
![(E)\rightarrow f(x)=x^2\\\\f(x_(1))=(x_(1))^2\\\\f(x_(2))=(x_(2))^2\\\\f(x_(1))+f(x_(2))=(x_(1))^2+(x_(2))^2\\\\f(x_(1)+x_(2))=[x_(1)+x_(2)]^2\\eq f(x_(1))+f(x_(2))](https://img.qammunity.org/2017/formulas/mathematics/high-school/ttiqf8lpyd0nyysffm75bvgpi42xrmevo5.png)
This function does not define f.
Option B: f(x)=2x , defines f.