Answer:
B.
Explanation:
To find the right exponential function, we can just take x-values an replace them into the given functions. The one that give the correct y-values will be the answer.
For
 , let's see which function gives
, let's see which function gives
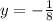

You can observe that function A is not the correct one, because it gives a positive result. However, function B can actually be the answer, because it woud give the same y-value than A but negative, as we need. Let's see

Let's evalute for
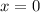
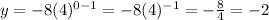
Which is right.
Therefore, the right answer is B.