Answer:
t(n) = 8n - 7
Explanation:
Formula for Arithmetic Sequence: t(n) = (CD)n + t(0)
- t(n) is the value of the term
- CD is a Common Difference, more about that soon
- n is the term number
- t(0) is the 0th term (the first value of all sequences is the first term)
Solve: Common Difference
Just like how you would solve for slope, you would solve for the CD
- CD = (term value - previous term value)/(term # - previous term #)
- CD = (9 - 1)/(2 - 1)
- CD = 8/1
- CD = 8
Now, we have the equation : t(n) = 8n + t(0)
Now we have to solve for t(0), the y-intercept of the 0th term
Solve: t(0)
Do this the same way you would solve for b in y = mx + b
- t(n) = (CD)n + t(0)
- 1 = 8(1) + t(0) <= Input output for t(n), and term number for n
- 1 = 8 + t(0)
- -7 = t(0)
Our final equation is
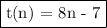
-Chetan K