Answer:
Coordinates of Mid Point of ST is ( h , 0 ) and x-coordinate of R is
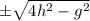 .
.
Explanation:
Given: Coordinate of S ( 0 , 0 ) , Coordinate of T ( 2h , 0 )
y-coordinate of R = g
Coordinates of Mid point of ST =
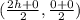
= ( h , 0 )
let x-coordinate of point R be x
Distance of RS = Distance of ST
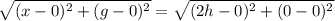
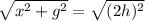
Squaring both sides, we get

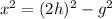
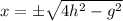
So, x-coordinate of R is
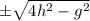
Therefore, Coordinates of Mid Point of ST is ( h , 0 ) and x-coordinate of R is
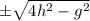 .
.