The first thing we are going to do for this case is define variables.
We have then:
w: width
l: length
The perimeter is given by:
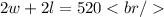
The area is given by:

The area as a function of a variable is:

Rewriting we have:
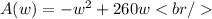
To obtain the maximum area, we derive:
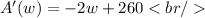
We equal zero and clear the value of w:
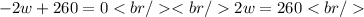
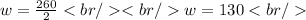
Then, the length is given by:

Finally, the maximum area obtained is:

Answer:
A retangle that maximizes the enclosed area has a length of 130 yards and a width of 130 yards.
The maxium area is 16900 square yards