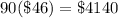Question

Solve. If there are X teams in a sports league and all the teams play each other twice, a total of N(x) gamers are played, where N(x)=x^2-x. A soccer league has 10 teams, each of which plays the others twice. If the league pays $46 per game for the field and officials, how much will it cost to play the entire schedule?

Answer 1

`\$4140`

Explanation:

According to the problem, x refers to teams, and
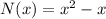`N(x)=x^(2)-x` represents numbers of games played.

So, if there are 10 teams, we just have to replace this value for the x and calculate the number of games. Once we have it, we multiply all games by $46, which is the cost per game.

`N(x)=x^(2) -x\\N(10)=(10)^(2)-10=100-10=90`

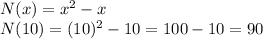
This means that in the entire schedule there are 90 games. If each one costs $46, the whole schedule will cost:

`90(\$46)=\$4140`

Answer 2

number of games is 90, so cost is

90×46=4140