Answer:
Option C is correct.
By the Subtraction Property of Equality.
Step-by-step explanation:
Supplementary Angles: Two angles are Supplementary if the sum of the measure of angles is 180 degree.
Given:

 {By definition of supplementary angle} .......[1]
{By definition of supplementary angle} .......[1]
Transitive Property of equality:
If a=b and
b = c,
then a = c
By the transitive property,
[1} ⇒
 ......[2]
......[2]
Subtraction property of equality states that you subtract the same number from both sides of an equation.
Subtract
 from both the sides in [2];
from both the sides in [2];
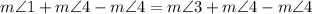
Simplify:
 {By subtraction property of equality}
{By subtraction property of equality}
Therefore, the only phrase which completes the proof is; by the subtraction property of equality