Answer:
The first 4 terms of the sequence are: 3, 9, 81, 6561
Explanation:
We are given the following recursive function:
![f(n) = [f(n-1)]^(2)](https://img.qammunity.org/2022/formulas/mathematics/college/s2nzdyrusqmxako80khqi64ldwkaawez6c.png)
And the following initial condition:
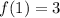
The second term of the sequence is:
![f(2) = [f(2-1)]^(2) = f(1)^2 = 3^2 = 9](https://img.qammunity.org/2022/formulas/mathematics/college/oc7tvbig49wwc6zs3u03e7md695atvdic6.png)
The third term of the sequence is:
![f(3) = [f(3-1)]^(2) = f(2)^2 = 9^2 = 81](https://img.qammunity.org/2022/formulas/mathematics/college/e769mbqxisvsuecxuvj5bxeqzwiwcaplpa.png)
The fourth term of the sequence is:
![f(4) = [f(4-1)]^(2) = f(3)^2 = 81^2 = 6561](https://img.qammunity.org/2022/formulas/mathematics/college/skj8pnwjcguogq6rlpb74j0tbdrpqlkxtj.png)
The first 4 terms of the sequence are: 3, 9, 81, 6561