Question

write the first 4 terms of the sequence defined by its given rule 5. f(1) = 7, f(n) = -4.f(n - 1) + 15

Answer 1

The first 4 terms of the sequence are: 3, 9, 81, 6561

Explanation:

We are given the following recursive function:

`f(n) = [f(n-1)]^(2)`

And the following initial condition:

`f(1) = 3`

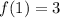
The second term of the sequence is:

`f(2) = [f(2-1)]^(2) = f(1)^2 = 3^2 = 9`

The third term of the sequence is:

`f(3) = [f(3-1)]^(2) = f(2)^2 = 9^2 = 81`

The fourth term of the sequence is:

`f(4) = [f(4-1)]^(2) = f(3)^2 = 81^2 = 6561`

The first 4 terms of the sequence are: 3, 9, 81, 6561