Answer:
When A = 48, the polynomial
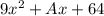 a perfect square trinomial.
a perfect square trinomial.
Explanation:
Given : the polynomial
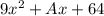
We have to find the value of A that makes the polynomial a perfect square trinomial.
For a trinomial to be a perfect square trinomial when it can be written in form of a perfect square as

Consider the given polynomial
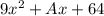
Comparing the given polynomial with the right side of the above identity,
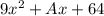 can be written as
can be written as
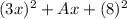
We have,
a = 3x , b = 8
also , 2ab = Ax
2(3x)(8) = Ax
⇒ 48 = A
Thus, When A = 48, the polynomial
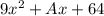 a perfect square trinomial.
a perfect square trinomial.