Question

The sum of two terms of gp is 6 and that of first four terms is 15/2.Find the sum of first six terms.​

Answer 1

Given:

The sum of two terms of GP is 6 and that of first four terms is
`(15)/(2).`

To find:

The sum of first six terms.​

Solution:

We have,

`S_2=6`

`S_4=(15)/(2)`

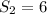
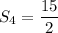
Sum of first n terms of a GP is

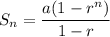`S_n=(a(1-r^n))/(1-r)` ...(i)

Putting n=2, we get

`S_2=(a(1-r^2))/(1-r)`

`6=(a(1-r)(1+r))/(1-r)`

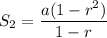
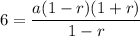
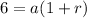`6=a(1+r)` ...(ii)

Putting n=4, we get

`S_4=(a(1-r^4))/(1-r)`

`(15)/(2)=(a(1-r^2)(1+r^2))/(1-r)`

`(15)/(2)=(a(1+r)(1-r)(1+r^2))/(1-r)`

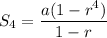
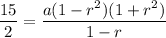
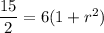`(15)/(2)=6(1+r^2)` (Using (ii))

Divide both sides by 6.

`(15)/(12)=(1+r^2)`

`(5)/(4)-1=r^2`

`(5-4)/(4)=r^2`

`(1)/(4)=r^2`

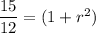
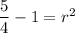
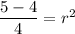
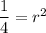
Taking square root on both sides, we get

`\pm \sqrt{(1)/(4)}=r`

`\pm (1)/(2)=r`

`\pm 0.5=r`

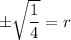
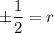
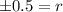
Case 1: If r is positive, then using (ii) we get

`6=a(1+0.5)`

`6=a(1.5)`

`(6)/(1.5)=a`

`4=a`

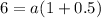
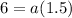
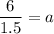
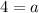
The sum of first 6 terms is

`S_6=(4(1-(0.5)^6))/((1-0.5))`

`S_6=(4(1-0.015625))/(0.5)`

`S_6=8(0.984375)`

`S_6=7.875`

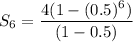
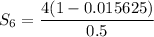
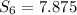
Case 2: If r is negative, then using (ii) we get

`6=a(1-0.5)`

`6=a(0.5)`

`(6)/(0.5)=a`

`12=a`

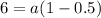
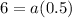
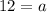
The sum of first 6 terms is

`S_6=(12(1-(-0.5)^6))/((1+0.5))`

`S_6=(12(1-0.015625))/(1.5)`

`S_6=8(0.984375)`

`S_6=7.875`

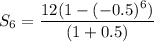
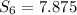
Therefore, the sum of the first six terms is 7.875.