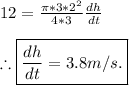Answer:
the rate of change is 3.8m/s
Explanation:
The volume of the right circular cone is

The rate of change of volume is
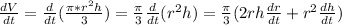
In order to proceed further we have to define r in terms of h so tht we can compute the derivative above.
The ratio between h and r is
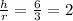
Therefore
 .
.
We plug that into the derivative above and get:
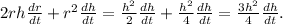
Thus

Now for the numerical part.
The rate of change of volume
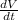 is
is
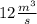 , so when the water is 2 meters deep
, so when the water is 2 meters deep
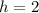 , therefore:
, therefore: