Question

A farming community begins with one resident. Then every year, the number of residents multiplies by 10 Write an expression using an exponent to

represent the number of residents in the community after 5 years

Answer 1

After 10 years , the number of residents in the community = 100,007.45

Explanation:

Let P be the population of a farming community.

As we know that,

Exponential Growth model is :

P(t) = P₀
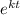`e^(kt)` ........(1)

where P₀ is the initial state , k is the growth constant.

As given,

A farming community begins with one resident.

⇒At t = 0 , P(t) = 1

∴ Put t = 0 in equation (1), we get

1 = P₀
`e^(0)`

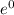
⇒1 = P₀

∴ equation (1) becomes

P(t) =
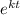`e^(kt)` ......(2)

As given, every year, the number of residents multiplies by 10

⇒At t = 1 , P(t) = 10

∴ Put t = 1 in equation (2), we get

10 =
`e^(k)`

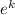
Taking ln both side we get

ln(10) = ln(
`e^(k)` )

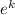⇒2.3026 = k

∴ equation (2) becomes

P(t) =
`e^(2.3026t )`

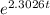
Now, we have to find the population at t = 5

⇒P(5) =
`e^(5(2.3026) = e^(11.513) = 100,007.45`

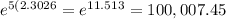
So, we get

After 10 years , the number of residents in the community = 100,007.45