Question

A hazard sign has 3 identical

parallelogram-shaped stripes as shown.

Charles must outline each stripe with

reflective tape. Is one roll of 144 inches

of tape enough to finish the job?

Answer 1

Answer and Explanation: To know how much tape he will need, we have to calculate the perimeter of each parallelogram-shaped stripe.

Perimeter is the sum of all the sides of a figure.

For a parallelogram:

P = 2*length + 2*width

So, we need to determine width and length of the stripe.

Width is 3 inches. Length is the hypotenuse of the right triangle, whose sides are 6 and 18 inches. Then, length is

`h=\sqrt{18^(2)+6^(2)}`

`h=√(360)`

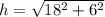
h = 19 in

Perimeter of the first stripe is

P = (2*19) + (2*3)

P = 44 inches

The hazard sign has 3 stripes. So total perimeter is

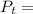`P_(t)=` 44 + 44 + 44

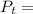`P_(t)=` 132 inches

To outline the parallelogram-shaped stripes, Charles need a total of 132 inches of tape. Since one roll has 144 inches, he will have enough tape to finish the job.