Answer:
a) The ductility = -30.12%
the negative sign means reduction
Therefore, there is 30.12% reduction
b) the true stress at fracture is 658.26 Mpa
Step-by-step explanation:
Given that;
Original diameter
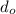 = 12.8 mm
= 12.8 mm
Final diameter
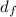 = 10.7
= 10.7
Engineering stress
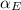 = 460 Mpa
= 460 Mpa
a) determine The ductility in terms of percent reduction in area;
Ai = π/4(
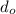 )² ; Ag = π/4(
)² ; Ag = π/4(
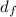 )²
)²
% = π/4 [ ( (
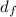 )² - (
)² - (
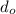 )²) / ( π/4 (
)²) / ( π/4 (
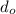 )²) ]
)²) ]
= ( (
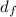 )² - (
)² - (
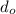 )²) / (
)²) / (
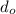 )² × 100
)² × 100
we substitute
= [( (10.7)² - (12.8)²) / (12.8)² ] × 100
= [(114.49 - 163.84) / 163.84 ] × 100
= - 0.3012 × 100
= -30.12%
the negative sign means reduction
Therefore, there is 30.12% reduction
b) The true stress at fracture;
True stress
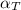 =
=
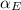 ( 1 +
( 1 +
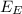 )
)
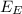 is engineering strain
is engineering strain
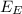 = dL / Lo
= dL / Lo
= (do² - df²) / df² = (12.8² - 10.7²) / 10.7² = (163.84 - 114.49) / 114.49
= 49.35 / 114.49
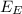 = 0.431
= 0.431
so we substitute the value of
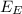 into our initial equation;
into our initial equation;
True stress
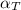 = 460 ( 1 + 0.431)
= 460 ( 1 + 0.431)
True stress
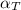 = 460 (1.431)
= 460 (1.431)
True stress
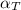 = 658.26 Mpa
= 658.26 Mpa
Therefore, the true stress at fracture is 658.26 Mpa