Answer:
a) The x coordinate of the third mass is -1.562 meters.
b) The y coordinate of the third mass is -0.944 meters.
Step-by-step explanation:
The center of mass of a system of particles (
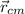 ), measured in meters, is defined by this weighted average:
), measured in meters, is defined by this weighted average:
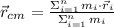 (1)
(1)
Where:
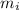 - Mass of the i-th particle, measured in kilograms.
- Mass of the i-th particle, measured in kilograms.
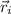 - Location of the i-th particle with respect to origin, measured in meters.
- Location of the i-th particle with respect to origin, measured in meters.
If we know that
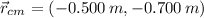 ,
,
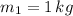 ,
,
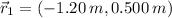 ,
,
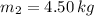 ,
,
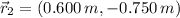 and
and
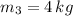 , then the coordinates of the third particle are:
, then the coordinates of the third particle are:
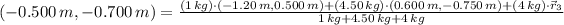
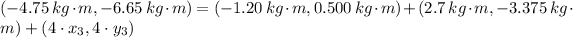
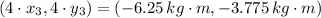
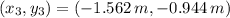
a) The x coordinate of the third mass is -1.562 meters.
b) The y coordinate of the third mass is -0.944 meters.