Question

The accompanying specific gravity values describe various wood types used in construction. 0.320.350.360.360.370.380.400.400.40 0.410.410.420.420.420.420.420.430.44 0.450.460.460.470.480.480.490.510.54 0.540.550.580.630.660.660.670.680.78 Construct a stem-and-leaf display using repeated stems. (Enter numbers from smallest to largest separated by spaces. Enter NONE for stems with no values.)

Answer 1

`\begin{array}{ccc}{Steam} & {\vert} & {Leaf} \ \\ \\ {0.3} & {\vert} & {2\ 5\ 6\ 6\ 7\ 8} \ \\ \\{0.4} & {\vert} & {0\ 0\ 0\ 1\ 1\ 2\ 2\ 2\ 2\ 2\ 3\ 4\ 5\ 6\ 6\ 7\ 8\ 8\ 9} \ \\ \ \\ {0.5} & {\vert} & {1\ 4\ 4\ 5\ 8} \ \\ \ \\ {0.6} & {\vert} & {3\ 6\ 6\ 7\ 8} \ \\ \ \\ {0.7} & {\vert} & {8} \ \ \end{array}`

Step-by-step explanation:

Given

`0.32,\ 0.35,\ 0.36,\ 0.36,\ 0.37,\ 0.38,\ 0.40,\ 0.40,\ 0.40,\ 0.41,`

`0.41,\ 0.42,\ 0.42,\ 0.42,\ 0.42,\ 0.42,\ 0.43,\ 0.44,\ 0.45,\ 0.46,`

`0.46,\ 0.47,\ 0.48,\ 0.48,\ 0.49,\ 0.51,\ 0.54,\ 0.54,\ 0.55,`

`0.58,\ 0.63,\ 0.66,\ 0.66,\ 0.67,\ 0.68,\ 0.78.`

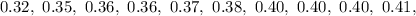
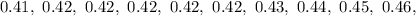
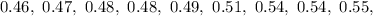
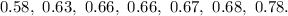
Required

Plot a steam and leaf display for the given data

Start by categorizing the data by their tenth values:

`0.32,\ 0.35,\ 0.36,\ 0.36,\ 0.37,\ 0.38.`

`0.40,\ 0.40,\ 0.40,\ 0.41,\ 0.41,\ 0.42,\ 0.42,\ 0.42,\ 0.42,\ 0.42,`

`0.43,\ 0.44,\ 0.45,\ 0.46,\ 0.46,\ 0.47,\ 0.48,\ 0.48,\ 0.49.`

`0.51,\ 0.54,\ 0.54,\ 0.55,\ 0.58.`

`0.63,\ 0.66,\ 0.66,\ 0.67,\ 0.68.`

`0.78.`

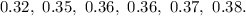
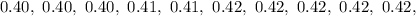
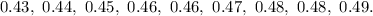
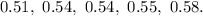
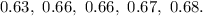
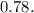
The 0.3's is will be plotted as thus:

`\begin{array}{ccc}{Steam} & {\vert} & {Leaf} \ \\ {0.3} & {\vert} & {2\ 5\ 6\ 6\ 7\ 8} \ \ \end{array}`

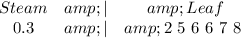
The 0.4's is as follows:

`\begin{array}{ccc}{Steam} & {\vert} & {Leaf} \ \\ {0.4} & {\vert} & {0\ 0\ 0\ 1\ 1\ 2\ 2\ 2\ 2\ 2\ 3\ 4\ 5\ 6\ 6\ 7\ 8\ 8\ 9} \ \ \end{array}`

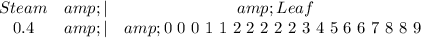
The 0.5's is as follows:

`\begin{array}{ccc}{Steam} & {\vert} & {Leaf} \ \\ {0.5} & {\vert} & {1\ 4\ 4\ 5\ 8} \ \ \end{array}`

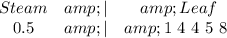
The 0.6's is as thus:

`\begin{array}{ccc}{Steam} & {\vert} & {Leaf} \ \\ {0.6} & {\vert} & {3\ 6\ 6\ 7\ 8} \ \ \end{array}`

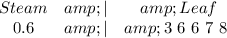
Lastly, the 0.7's is as thus:

`\begin{array}{ccc}{Steam} & {\vert} & {Leaf} \ \\ {0.7} & {\vert} & {8} \ \ \end{array}`

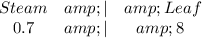
The combined steam and leaf plot is:

`\begin{array}{ccc}{Steam} & {\vert} & {Leaf} \ \\ \\ {0.3} & {\vert} & {2\ 5\ 6\ 6\ 7\ 8} \ \\ \\{0.4} & {\vert} & {0\ 0\ 0\ 1\ 1\ 2\ 2\ 2\ 2\ 2\ 3\ 4\ 5\ 6\ 6\ 7\ 8\ 8\ 9} \ \\ \ \\ {0.5} & {\vert} & {1\ 4\ 4\ 5\ 8} \ \\ \ \\ {0.6} & {\vert} & {3\ 6\ 6\ 7\ 8} \ \\ \ \\ {0.7} & {\vert} & {8} \ \ \end{array}`