Answer:
Symmetry about y-axis
Explanation:
If f(x) is a even function and (6,8) is one the points on the graph of f(x).
Even Function: It makes symmetry about y-axis. The value of y is same from origin to left side and right side of y-axis.
Even function:
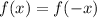
For even function, if (6,8) point on f(x) then (-6,8) must be on f(x).
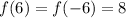
The value of y=8 is same 6 unit from left and right of y-axis 6.
Both points are on function because it is symmetry about y-axis for even function.