we have
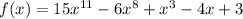
we know that
The Rational Root Theorem states that when a root 'x' is written as a fraction in lowest terms
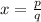
p is an integer factor of the constant term, and q is an integer factor of the coefficient of the first monomial.
So
in this problem
the constant term is equal to

and the first monomial is equal to
 -----> coefficient is
-----> coefficient is

So
possible values of p are

possible values of q are
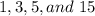
therefore
the answer is
The all potential rational roots of f(x) are
(+/-)
 ,(+/-)
,(+/-)
 ,(+/-)
,(+/-)
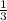 ,(+/-)
,(+/-)
 ,(+/-)
,(+/-)
 ,(+/-)
,(+/-)
