Question

Which exponential function is represented by the values in the table?

f(x) = 3(2x)

f(x) = 2(2x)

f(x) = 3(3x)

f(x) = 2(3x)

Answer 1

The function
`f(x) = 3( {2}^(x) )`.

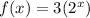Explanation:

Given : Table for x and f(x).

To find : Which exponential function is represented by the values in the table.

Solution : Let the exponential function that is represented by the values in the table be of the form,

`f(x) = a( {b}^(x) )`

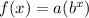
On plugging the values from table (0,3)

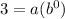`3 = a( {b}^(0) )` we get ,

3 = a.

tex]f(x) = 3( {b}^{x} )[/tex]

To find value of b we substituting other point from table (1,6)

tex]6 = 3( {b}^{1} )[/tex].

2 = b.

Therefore , the function
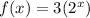`f(x) = 3( {2}^(x) )`.

Answer 2

ANSWER

The exponential function is

`f(x) = 3( {2}^(x) )`

EXPLANATION

Let the exponential function that is represented by the values in the table be of the form,


`f(x) = a( {b}^(x) )`

The points in the table must satisfy this exponential function.


We substitute the point,


`(0,3)`

to get,



`3 = a( {b}^(0) )`



This implies that,



`3 = a( 1 )`



`3 = a`


Our function now becomes,


`f(x) = 3( {b}^(x) )`


We gain, plug in another point yo find the value of b too.


Let us substitute

`(1,6)`


This implies that,


`6= 3( {b}^(1) )`


We divide through by 3 to obtain,


`2 = b`


Therefore the function is,



`f(x) = 3( {2}^(x) )`



The correct answer is A.