Question

Which graph represents the function f(x)=5lnx?

Answer 1

The first graph (top-left) is the correct graph.

Please, also check the attached graph.

Explanation:

Given the function

`f\left(x\right)=5\:lnx`

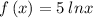
First, we should determine the x and y-intercepts.

Determining the y-intercept:

We know that the value of the y-intercept can be determined by setting x = 0 and determining the corresponding value of y.

Thus,

substitute x = 0 in the function

y = lnx

y = ln(0)

y = undefined

Therefore, at x = 0, the value of y becomes undefined.

Hence, None is the y-intercept.

Determining the x-intercept:

We know that the value of the x-intercept can be determined by setting y = 0 and determining the corresponding value of x.

Thus,

substitute y = 0 in the function

0 = ln(x)

Flipe the equation

ln(x) = 0

Solve algorithm

ln(x) = 0

Take exponent of both sides

`\:e^(ln\left(x\right))=e^0`

`x\:=e^0`

`x = 1`

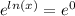
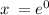
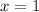
Thus, the point of x-intercept is: (0, 1)

Conclusion:

Now, if we carefully check the graph options, we can easily figure out that the first graph (top-left) correctly displays the x and y-intercepts.

It is clear from the graph that:

at x = 0, y is heading towards -ve infinity.

at y = 0, x = 1

Therefore, the first graph (top-left) is the correct graph.

Please, also check the attached graph.