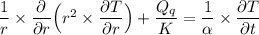Question

Write the heat equation for each of the following cases:

a. A wall, steady state, stationary, one-dimensional, incompressible and no energy generation.
b. A wall, transient, stationary, one-dimensional, incompressible, constant k with energy generation.
c. A cylinder, steady state, stationary, two-dimensional (radial and axial), constant k, incompressible, with no energy generation.
d. A wire moving through a furnace with constant velocity, steady state, one-dimensional (axial), incompressible, constant k and no energy generation.
e. A sphere, transient, stationary, one-dimensional (radial), incompressible, constant k with energy generation.

Answer 1

Step-by-step explanation:

a) the steady-state, 1-D incompressible and no energy generation equation can be expressed as follows:

`(\partial^2T)/(\partial x^2)= \ 0 \ ; \ if \ T = f(x) \\ \\ (\partial^2T)/(\partial y^2)= \ 0 \ ; \ if \ T = f(y) \\ \\ (\partial^2T)/(\partial z^2)= \ 0 \ ; \ if \ T = f(z)`

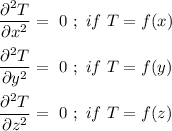
b) For a transient, 1-D, constant with energy generation

suppose T = f(x)

Then; the equation can be expressed as:

`(\partial^2T)/(\partial x^2) + (Q_g)/(k) = (1)/(\alpha) (dT)/(dC)`

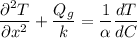
where;

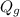`Q_g` = heat generated per unit volume

`\alpha` = Thermal diffusivity

c) The heat equation for a cylinder steady-state with 2-D constant and no compressible energy generation is:

`(1)/(r)* (\partial)/(\partial r )( r* (\partial \ T )/(\partial \ r)) + (\partial^2 T)/(\partial z^2 )= 0`

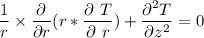
where;

The radial directional term =
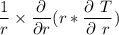`(1)/(r)* (\partial)/(\partial r )( r* (\partial \ T )/(\partial \ r))` and the axial directional term is
`(\partial^2 T)/(\partial z^2 )`

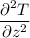
d) The heat equation for a wire going through a furnace is:

`(\partial ^2 T)/(\partial z^2) = (1)/(\alpha)\Big [(\partial ^2 T)/(\partial ^2 t)+ V_z (\partial ^2T)/(\partial ^2z) \Big ]`

since;

the steady-state is zero, Then:

`(\partial ^2 T)/(\partial z^2) = (1)/(\alpha)\Big [ V_z (\partial ^2T)/(\partial ^2z) \Big ]`'

e) The heat equation for a sphere that is transient, 1-D, and incompressible with energy generation is:

`(1)/(r) * (\partial)/(\partial r) \Big ( r^2 * (\partial T)/(\partial r) \Big ) + (Q_q)/(K) = (1)/(\alpha)* (\partial T)/(\partial t)`