Answer:
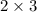
Explanation:
We have been given an expression and we are asked to find the cube root of our given expression.
![\sqrt[3]{8* 27}](https://img.qammunity.org/2017/formulas/mathematics/high-school/2k3okd6dq61zoz12lsuyjprx6i6qolgl0v.png)
Using the property for radicals
![\sqrt[n]{a* b}=\sqrt[n]{a}* \sqrt[n]{b}](https://img.qammunity.org/2017/formulas/mathematics/high-school/nr493hr5vd9xy9znv8iqniych4stuel7vh.png) we can rewrite our expression as:
we can rewrite our expression as:
![\sqrt[3]{8}* \sqrt[3]{27}](https://img.qammunity.org/2017/formulas/mathematics/high-school/lmyijo7gc8lcwmrbxrwkvomrpyikx83gvh.png)
We can rewrite terms of our given expression as:
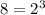
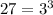
Now, we will substitute back these terms back in our given expression.
![\sqrt[3]{2^3}* \sqrt[3]{3^3}](https://img.qammunity.org/2017/formulas/mathematics/high-school/bim4jnf0yirarpps934i6chq7195yrki8l.png)
Using exponent property
![\sqrt[n]{x^m}=x^{(m)/(n)}](https://img.qammunity.org/2017/formulas/mathematics/high-school/39nad68wsvvpe647hmunl4gfo4x1liknoh.png) , we can rewrite our expression as:
, we can rewrite our expression as:
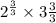
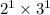
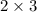
Therefore, the cube root of our given expression is
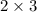 .
.