Question

What is the cube root of 8x27

Answer 1

I hope this helps you

Answer 2

`2* 3`

Explanation:

We have been given an expression and we are asked to find the cube root of our given expression.

`\sqrt[3]{8* 27}`

Using the property for radicals
`\sqrt[n]{a* b}=\sqrt[n]{a}* \sqrt[n]{b}` we can rewrite our expression as:

`\sqrt[3]{8}* \sqrt[3]{27}`

We can rewrite terms of our given expression as:

`8=2^3`

`27=3^3`

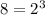
Now, we will substitute back these terms back in our given expression.

`\sqrt[3]{2^3}* \sqrt[3]{3^3}`

Using exponent property
`\sqrt[n]{x^m}=x^{(m)/(n)}`, we can rewrite our expression as:

`2^{(3)/(3)}* 3{(3)/(3)}`

`2^(1)* 3^(1)`

`2* 3`

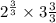
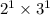
Therefore, the cube root of our given expression is
`2* 3`.