Answer:
3.28 degree
Step-by-step explanation:
We are given that
Distance between the ruled lines on a diffraction grating, d=1900nm=
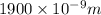
Where
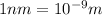
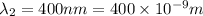
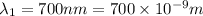
We have to find the angular width of the gap between the first order spectrum and the second order spectrum.
We know that
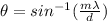
Using the formula
m=1
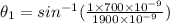
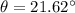
Now, m=2
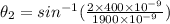
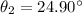
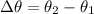
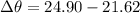

Hence, the angular width of the gap between the first order spectrum and the second order spectrum=3.28 degree