Question

The distance between the ruled lines on a diffraction grating is 1900 nm. The grating is illuminated at normal incidence with a parallel beam of white light in the 400 nm to 700 nm wavelength band. What is the angular width of the gap between the first order spectrum and the second order spectrum

Answer 1

3.28 degree

Step-by-step explanation:

We are given that

Distance between the ruled lines on a diffraction grating, d=1900nm=
`1900* 10^(-9)m`

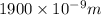
Where
`1nm=10^(-9) m`

`\lambda_2=400nm=400*10^(-9)m`

`\lambda_1=700nm=700* 10^(-9)m`

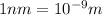
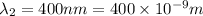
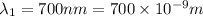
We have to find the angular width of the gap between the first order spectrum and the second order spectrum.

We know that

`\theta=sin^(-1)((m\lambda)/(d))`

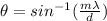
Using the formula

m=1

`\theta_1=sin^(-1)((1*700* 10^(-9))/(1900* 10^(-9)))`

`\theta=21.62^(\circ)`

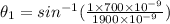
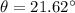
Now, m=2

`\theta_2=sin^(-1)((2*400* 10^(-9))/(1900* 10^(-9)))`

`\theta_2=24.90^(\circ)`

`\Delta \theta=\theta_2-\theta_1`

`\Delta \theta=24.90-21.62`

`\Delta \theta=3.28^(\circ)`

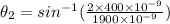
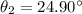
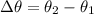
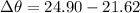
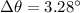
Hence, the angular width of the gap between the first order spectrum and the second order spectrum=3.28 degree