Answer:
A load of 32000 cubic feet fill the silo to height 45.252 feet.
Explanation:
Height of silo = 60 feet
Radius of silo = 15 feet
Suppose silo in in the shape of cylinder
Volume of grain in silo =
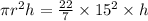
Volume of grain in silo =
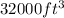
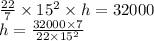
h=45.252 feet
Hence A load of 32000 cubic feet fill the silo to height 45.252 feet.