Question

What is the area of the half circle below?2 Pi 4pi 8pi 16pi

Answer 1

A = 8π cm²

Explanation:

The area (A) of a circle is calculated as

A = πr² ( r is the radius )

Here diameter = 8 , then r = 8 ÷ 2 = 4

The area of half a circle is then

A =
`(1)/(2)` π × 4² =
`(1)/(2)` × π × 16 = 8π cm²

Answer 2

The area of semicircle is 8π cm².

Step-by-step explanation:

`\large{\tt{\underline{\underline{\red{SOLUTION}}}}}`

Given :

Here we have given that the diameter of a semicircle is 8 cm. So, the radius will be 8/2 = 4 cm.

Calculating :

Now, finding the area of semicircle by substituting the values in the formula :

`{\longrightarrow{\pmb{\sf{Area_((Semicircle)) = (1)/(2)( \pi {r}^(2))}}}}`

`{\longrightarrow{\sf{Area_((Semicircle)) = (1)/(2)\Big( \pi {(4)}^(2)\Big)}}}`

`{\longrightarrow{\sf{Area_((Semicircle)) = (1)/(2)\Big( \pi {(4 * 4)}\Big)}}}`

`{\longrightarrow{\sf{Area_((Semicircle)) = (1)/(2)\Big( \pi {(16)}\Big)}}}`

`{\longrightarrow{\sf{Area_((Semicircle)) = (1)/(2)\Big( \pi * 16\Big)}}}`

`{\longrightarrow{\sf{Area_((Semicircle)) = (1)/(2)\big( 16\pi \big)}}}`

`{\longrightarrow{\sf{Area_((Semicircle)) = (1)/(2) * 16\pi}}}`

`{\longrightarrow{\sf{Area_((Semicircle)) = \frac{1}{\cancel{2}} * \cancel{16}\pi}}}`

`{\longrightarrow{\sf{Area_((Semicircle)) = 1 * 8\pi}}}`

`{\longrightarrow{\sf{Area_((Semicircle)) = 8\pi}}}`

`\star{\underline{\boxed{\sf{ \purple{Area_((Semicircle)) = 8\pi \: cm^2}}}}}`

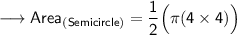
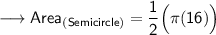
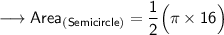
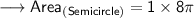
Hence, the area of semicircle is 8π cm².

`\rule{300}{2.5}`