Question

The total profit made by an engineering firm is given by the function p=x^2 - 24x +5000 where x is the number of clients the firm has and p is the profit.

1. Find the maximum profit made by the company.

2. How many clients are necessary to reach the profit outlined in part one?

Answer 1

`5144`

`12`

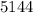
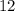
Explanation:

The function
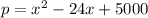`p=x^2-24x+5000` is incorrect as its roots are imaginary
`b^2-4ac=576-4* 5000=-19424<0`.

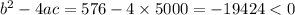So, the correct function is

`p=-x^2+24x+5000`

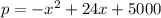
Differentiating with respect to
`x` we get

`p'=-2x+24`

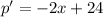
Equating with zero

`0=-2x+24\\\Rightarrow x=(24)/(2)\\\Rightarrow x=12`

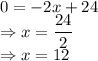
Double derivative of the function

`p''=-2<0`

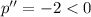
So, the function is maximum at
`x=12`

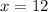
Maximum profit is

`p=-x^2+24x+5000=-12^2+24* 12+5000\\\Rightarrow p=5144`

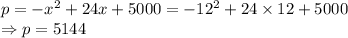
The maximum profit made by the company is
`5144`

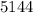
The number of clients required to make the maximum profit is
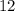`12`.