Question

let m be a positive integer with n bit binary representation an-1 an-2 ... a1a0 with an-1=1 what are the smallest and largest values that m could have

Answer 1

Step-by-step explanation:

From the given information:

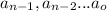`a_(n-1) , a_(n-2)...a_o` in binary is:

`a_(n-1)* 2^(n-1) + a_(n-2)}* 2^(n-2)+ ...+a_o`

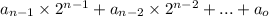
So, the largest number posses all
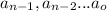`a_(n-1) , a_(n-2)...a_o` nonzero, however, the smallest number has
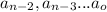`a_(n-2) , a_(n-3)...a_o` all zero.

∴

The largest = 11111. . .1 in n times and the smallest = 1000. . .0 in n -1 times

i.e.

`(11111111...1)_2 = ( 1 * 2^(n-1) + 1* 2^(n-2) + ... + 1 )_(10)`

`= (1(2^n-1))/(2-1)`

`\mathbf{=2^n -1}`

`(1000...0)_2 = (1 * 2^(n-1) + 0 * 2^(n-2) + 0 * 2^(n-3) + ... + 0)_(10)`

`\mathbf {= 2 ^(n-1)}`

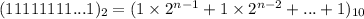
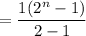
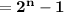
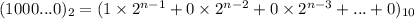
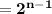
Hence, the smallest value is
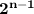`\mathbf{2^(n-1)}` and the largest value is
`\mathbf{2^(n)-1}`