Answer:

Explanation:
Volume of cylinder(V) is given by:

where,
r is the radius of the cylinder
h is the height of the cylinder.
As per the statement:
A cylinder has a radius of 5x + 2 and a height of 2x + 8
⇒r = 5x +2 units and h = 2x+8 units
Substitute in [1] we have;

Using the identity rule:
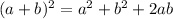
⇒

⇒

Combine like terms;
⇒

⇒

Therefore, in standard form best describes the total volume of the cylinder is:
