Answer:
3π square units.
Explanation:
We can use the disk method.
Since we are revolving around AB, we have a vertical axis of revolution.
So, our representative rectangle will be horizontal.
R₁ is bounded by y = 9x.
So, x = y/9.
Our radius since our axis is AB will be 1 - x or 1 - y/9.
And we are integrating from y = 0 to y = 9.
By the disk method (for a vertical axis of revolution):
![\displaystyle V=\pi \int_a^b [R(y)]^2\, dy](https://img.qammunity.org/2022/formulas/mathematics/college/u0k50mpvstnjwkzkvrzn9fj98a0t5isr5u.png)
So:

Simplify:
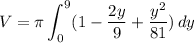
Integrate:
![\displaystyle V=\pi\Big[y-(1)/(9)y^2+(1)/(243)y^3\Big|_0^9\Big]](https://img.qammunity.org/2022/formulas/mathematics/college/nzmioa6qnixpd30waacyp9qi0ibji2xpfw.png)
Evaluate (I ignored the 0):
![\displaystyle V=\pi[9-(1)/(9)(9)^2+(1)/(243)(9^3)]=3\pi](https://img.qammunity.org/2022/formulas/mathematics/college/ngm7jsis5pny6wy6cge570vakatmniyjns.png)
The volume of the solid is 3π square units.
Note:
You can do this without calculus. Notice that R₁ revolved around AB is simply a right cone with radius 1 and height 9. Then by the volume for a cone formula:

We acquire the exact same answer.