184. A student estimated a mass to be 40 g. After carefully measuring, she found the actual mass to be 45 g. What is the percent of error?

Question

asked Apr 21, 2022 2.0k views

1 Answer

Shawn Azdam · Answer 1 · 2022-04-27T20:51:22+0000

Answer:

$\boxed {\boxed {\sf About \ 11 \%}}$

Explanation:

The formula for percent error is:

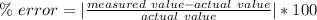
$\% \ error = | (measured \ value - actual \ value )/(actual \ value) | *100$

For this, the measured value is the estimation of 40 grams. The actual value is the true mass of 45 grams.

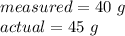
$measured = 40 \ g \\actual = 45 \ g$

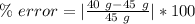
$\% \ error = | (40 \ g - 45 \ g )/(45 \ g ) | *100$

Solve the numerator.

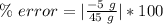
$\% \ error = | (-5 \ g )/(45 \ g ) | *100$

Divide.

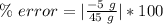
$\% \ error = | (-5 \ g )/(45 \ g ) | *100$

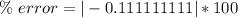
$\% \ error = | -0.111111111| *100$

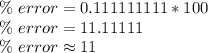
$\% \ error = 0.111111111*100\\\% \ error = 11.11111 \\\% \ error \approx 11$

The percent error is about 11%