Answer : The length of the side of an iron ingot (rectangular box) is 0.0233 cm.
Explanation : Given,
Width of rectangular box = 5.00 cm
Height of rectangular box = 5.00 cm
Mass of rectangular box = 4.578 g
Density of iron =
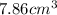
First we have to determine the volume of rectangular box.
Formula used :

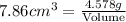

Now we have to determine the length of rectangular box.
Formula for volume of rectangle :

where,
V = volume of rectangular box
l = length of rectangular box
b = width of rectangular box
h = height of rectangular box
Now put all the given values in the above formula, we get:
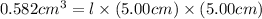
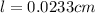
Therefore, the length of the side of an iron ingot (rectangular box) is 0.0233 cm.