Answer:
-- I don't know if you'll still need mine, but here's what I got --
1st (shaded) box = Area is 441
2nd (shaded) box = Area is 1,764
Explanation:
First of all, It stated, "To determine the area of the (shaded) portion" but it didn't mention the white box so I ignored it and pay attention only to the "shaded box" as mentioned in the assignment
1st (shaded) box
1. write it out like so,

2. next to get "x" alone subtract 7 to the other side once done you would have this,
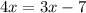
3. then subtract 3x to both sides...
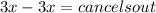 >>
>>
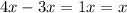 >> you're now left with,
>> you're now left with,
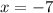
To find the area we need one more step...
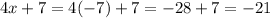 and
and
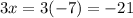 then multiply to get the area, negative crosses each other out once multiplying so -21 times -21 gives you 441
then multiply to get the area, negative crosses each other out once multiplying so -21 times -21 gives you 441
-------
2nd (shaded) box repeat from above
1.
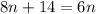
2.
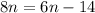
3.
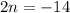 , here is different as there is still one more step, we need to divide to get "n" alone.
, here is different as there is still one more step, we need to divide to get "n" alone.
4.

Now plugin to get the area,
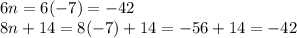 once multiplied you get 1,764
once multiplied you get 1,764
Once again I could be wrong but this is what I got after reading the little description from your attached assignment.