Answer:
The distance from point P, P(-2,4) to the given line y= 2x-2 is 1.56
Explanation:
We need to find the distance from point P to the given line
P(-2,4) , y= 2x-2
The formula used is:
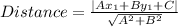
Where A, B and C are points of line i.e Ax+By+C=0
and x_1 and y_1 are points of P
So, y=2x-2 in Ax+By+C=0 is:
2x-y-2=0
A=2,
B=-1
C=1
Point given is P(-2,4)
x_1=-2
y_1=4
Putting values and finding distance

So, the distance from point P, P(-2,4) to the given line y= 2x-2 is 1.56