Question

Find the distance from point P to the given line

Answer 1

The distance from point P, P(-2,4) to the given line y= 2x-2 is 1.56

Explanation:

We need to find the distance from point P to the given line

P(-2,4) , y= 2x-2

The formula used is:
`Distance=(|Ax_1+By_1+C|)/(√(A^2+B^2) )`

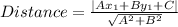
Where A, B and C are points of line i.e Ax+By+C=0

and x_1 and y_1 are points of P

So, y=2x-2 in Ax+By+C=0 is:

2x-y-2=0

A=2,

B=-1

C=1

Point given is P(-2,4)

x_1=-2

y_1=4

Putting values and finding distance

`Distance=(|Ax_1+By_1+C|)/(√(A^2+B^2) )\\Distance=(|2(-2)+-1(4)+1|)/(√((-2)^2+(4)^2) )\\Distance=(|-4-4+1|)/(√(4+16) )\\Distance=(|-7|)/(√(20))\\Distance=(7)/(√(20) )\\Distance=(7)/(4.5)\\Distance=1.56`

So, the distance from point P, P(-2,4) to the given line y= 2x-2 is 1.56