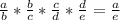
lets rewrite the equation so as to better understand why this equation is true..
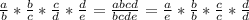
If both the numerator and the denominator are the same in a fraction, then that fraction is equivalent to 1. So we can rewrite the equation as such.
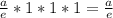
Since the b's, c's and d's cancel out, a/b*b/c*c/d*d/e=a/e