Question

The first and last terms of a 52-term arithmetic series are listed in the table. What is the sum of the series?

Term Number Term
1 1
52 154

Answer 1

sn = (n(a1 + a52)) / 2
n = 52
a1 = 1
a52 = 154

s52 = (52(1 + 154)) / 2
s52 = (52(155)) / 2
s52 = 8060/2
s52 = 4030 <==

Answer 2

Answer: 4030

Explanation:

We know that sum of an arithmetic series with first term as 'a' and the last term as 'l' is given by :-

`S_n=(n)/(2)(a+l)`, where n is the number of terms

In the given situation, the number of terms = 52

The first term = 1

The 52th term = 154

Then the sum of 52 terms ids given by :-

`S_(52)=(52)/(2)(1+154)\\\Rightarrow\ S_(52)=(26)(155)=4030`

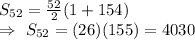
Hence, the sum of the series =4030