Question

In a beach town, 13% of the residents own boats. A random sample of 100 residents was selected. What is the probability that less than 11% of the residents in the sample own boats?

Find the z-table here.

Answer 1

0.276

Explanation:

got it right on edge

Answer 2

Approximately
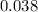`0.038` (or equivalently
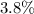`3.8\%`,) assuming that whether each resident owns boats is independent from one another.

Explanation:

Assume that whether each resident of this town owns boats is independent from one another. It would be possible to model whether each of the
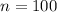`n = 100` selected residents owns boats as a Bernoulli random variable: for
`k = \lbrace 1,\, \dots,\, 100\rbrace`,
`X_k \sim \text{Bernoulli}(\underbrace{0.13}_(p))`.

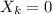`X_k = 0` means that the
`k`th resident in this sample does not own boats. On the other hand,
`X_k = 1` means that this resident owns boats. Therefore, the sum
`(X_1 + \cdots + X_(100))` would represent the number of residents in this sample that own boats.

Each of these
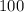`100` random variables are all independent from one another. The mean of each
`X_k` would be
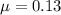`\mu = 0.13`, whereas the variance of each
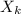`X_k\!` would be
`\sigma = p\, (1 - p) = 0.13 * (1 - 0.13) = 0.1131`.

The sample size of
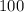`100` is a rather large number. Besides, all these samples share the same probability distribution. Apply the Central Limit Theorem. By this theorem, the sum
`(X_1 + \cdots + X_(100))` would approximately follow a normal distribution with:

• mean
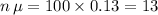  `n\, \mu = 100 * 0.13 = 13`, and
• variance
  `\sigma\, √(n) = p\, (1 - p)\, √(n) = 0.1131 * 10 = 1.131`.

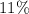`11\%` of that sample of
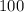`100` residents would correspond to
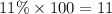`11\% * 100 = 11` residents. Calculate the
`z`-score corresponding to a sum of
`11`:

`\begin{aligned}z &= (11 - 13)/(1.131) \approx -1.77 \end{aligned}`.

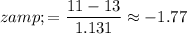The question is (equivalently) asking for
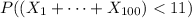`P( (X_1 + \cdots + X_(100)) < 11)`. That is equal to
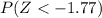`P(Z < -1.77)`. However, some
`z`-tables list only probabilities like
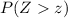`P(Z > z)`. Hence, convert
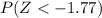`P(Z < -1.77)\!` to that form:

`\begin{aligned} & P( (X_1 + \cdots + X_(100)) < 11) \\ &= P(Z < -1.77) \\ &= 1 - P(Z >1.77) \end{aligned}`.

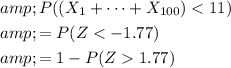Look up the value of
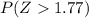`P(Z > 1.77)` on a
`z`-table:

`P(Z > 1.77) \approx 0.962`.

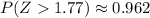Therefore:

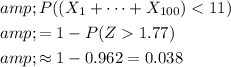`\begin{aligned} & P( (X_1 + \cdots + X_(100)) < 11) \\ &= 1 - P(Z >1.77) \\ &\approx 1 - 0.962 = 0.038 \end{aligned}`.