Answer:
we conclude that:

Hence, (1, 5) is the solution in interval notation.
Please also check the attached graph.
Explanation:
Given the inequality expression
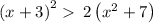
as
(x + 3)² = x² + 6x + 9
2(x² + 7) = 2x² + 14
so
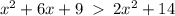
rewriting in the standard form
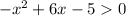
Factor -x² + 6x - 5: - (x - 1) (x - 5)
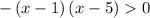
Multiply both sides by -1 (reverse the inequality)
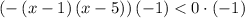
Simplify
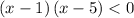
so
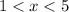
Therefore, we conclude that:

Hence, (1, 5) is the solution in interval notation.
Please also check the attached graph.