Question

Solve the inequality. use interval notion to state the solution (x+3)^2>2(x^2+7)

Answer 1

we conclude that:

`x^2+6x+9>2x^2+14\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:1<x<5\:\\ \:\mathrm{Interval\:Notation:}&\:\left(1,\:5\right)\end{bmatrix}`

Hence, (1, 5) is the solution in interval notation.

Please also check the attached graph.

Explanation:

Given the inequality expression

`\left(x+3\right)^2>\:2\left(x^2+7\right)`

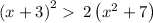
as

(x + 3)² = x² + 6x + 9

2(x² + 7) = 2x² + 14

so

`\:x^2+6x+9\:>\:2x^2+14`

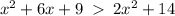
rewriting in the standard form

`-x^2+6x-5>0`

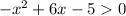
Factor -x² + 6x - 5: - (x - 1) (x - 5)

`-\left(x-1\right)\left(x-5\right)>0`

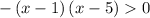
Multiply both sides by -1 (reverse the inequality)

`\left(-\left(x-1\right)\left(x-5\right)\right)\left(-1\right)<0\cdot \left(-1\right)`

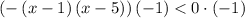
Simplify

`\left(x-1\right)\left(x-5\right)<0`

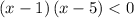
so

`1<x<5`

Therefore, we conclude that:

`x^2+6x+9>2x^2+14\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:1<x<5\:\\ \:\mathrm{Interval\:Notation:}&\:\left(1,\:5\right)\end{bmatrix}`

Hence, (1, 5) is the solution in interval notation.

Please also check the attached graph.