Question

A circle has a radius of 8 inches. Find the area of a sector of the circle if the sector has an arc that measures 45°.

2 sq. in.?
8 sq. in.?
16 sq. in.?

Answer 1

The area of the sector is 8π or 25.133 square inches.

Explanation:

The formula for area of a section is

`A=\pi r^2* ((\theta)/(360))`

Where, r is the radius of the circle and θ is the central angle.

It is given that the radius of the circle is 8 inches and the sector has an arc that measures 45°, it means the central angle is 45°.

`A=\pi (8)^2* ((45)/(360))`

`A=8\pi`

`A=25.1327412287`

`A\approx 25.133`

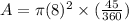
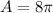
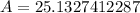
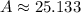
Therefore the area of the sector is 8π or 25.133 square inches.

Answer 2

The formula of the sector is expressed in the following expression:
Area = 0.5 * r^2 * theta
where r is the radius of the circle and theta is the angle in which the sector is measured and is expressed in radians. In this case, upon substitution
Area = 0.5*8^2 * 45 degrees * (pi/180 degrees)Area = 25.15 square inches