Question

The seventh and tenth terms of a geometric sequence are 7 and 21 respectively. What is the 13th term of this progression?

Answer 1

To find the 13th term of a geometric sequence with given seventh and tenth terms, calculate the common ratio, raise it to the appropriate power, and multiply it by the seventh term to find the value of the 13th term, which in this case is 63.

Step-by-step explanation:

The student asked for the 13th term of a geometric sequence where the seventh term is 7 and the tenth term is 21. The formula for the nth term of a geometric sequence is an = a1 × r(n-1), where a1 is the first term and r is the common ratio. Given the seventh term (a7) and the tenth term (a10), we can find the common ratio with the equation r3 = a10 / a7.

Dividing 21 by 7 gives us the common ratio r to the third power, meaning r3 = 3. Taking the cube root of 3, we find r = 31/3 which is the common ratio between consecutive terms. To find the 13th term (a13), we use the seventh term and multiply it by r6, since the 13th term is six terms away from the 7th term.

Calculating a13 gives 7 × 36/3 = 7 × 32 = 7 × 9 = 63. Therefore, the 13th term of this geometric progression is 63.

Answer 2

63

Step-by-step explanation:

Each term in a geometric sequence progresses by multiplying a constant (let us name it r).

Let us solve for this constant r in order to find the 13th term.

If the seventh term is 7, the tenth term would be 7*r*r*r, or
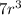`7r^(3)`. We also happen to know that the 10th term is 21. Let us make a new equation:

`7r^(3) =21\\r^(3)=3\\r= \sqrt[3]{3}`

or, approx. 1.442249570307408

Using the same logic, the 13th term would be 7*r*r*r*r*r*r, or
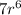`7r^(6)`. We may now substitute what we know, r, into this expression to obtain the 13th term:

`7*\sqrt[3]{3}^(6) = \\7*3^(2)=\\7*9=\\63`

Therefore, the 13th term of this progression is 63.

I hope this helps! Please let me know if you have any further questions :)