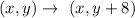Answer:
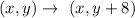
Explanation:
We know that a translation is a type of rigid motion that is used in geometry to trace a function that maps an object for a particular distance.
We know that the coordinate notation of translation a point (x,y) moved by h units right wards and k units upwards is given by :-

If there is only upward translation by k units then the rule for translation becomes :-

Thus, the mapping notation to describe a translation up 8 units is given by :-