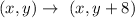Question

Use mapping notation to describe a translation up 8 units.

Answer 1

Describe the translation in words: (x, y) (x - 3, y + 7) =3 units to the left, 7 units up

Describe the translation as an ordered pair: 5 units to the right, 4 units down.
=(x, y)(x + 5, y – 4)

Describe the translation in words: (x, y) (x + 6, y – 2) =6 units to the right, 2 units down


Describe the translation as an ordered pair: 1 unit to the left, 8 units down
=(x, y) (x – 1, y – 8)

Answer 2

Answer:
`(x,y)\rightarrow\ (x,y+8)`

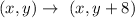
Explanation:

We know that a translation is a type of rigid motion that is used in geometry to trace a function that maps an object for a particular distance.

We know that the coordinate notation of translation a point (x,y) moved by h units right wards and k units upwards is given by :-

`(x,y)\rightarrow\ (x+h,y+k)`

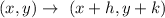
If there is only upward translation by k units then the rule for translation becomes :-

`(x,y)\rightarrow\ (x,y+k)`

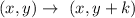
Thus, the mapping notation to describe a translation up 8 units is given by :-

`(x,y)\rightarrow\ (x,y+8)`